mardi 10 juin 2008
Usage des générateurs de nombres pseudo-aléatoires
Par haypo, mardi 10 juin 2008 à 00:00 :: Sécurité informatique
Exigences vis à vis d'un générateur de nombres pseudo-aléatoires
Les générateurs de nombres pseudo-aléatoires sont utilisés principalement à deux fins :
- Simulation : simulation physique, jeux vidéos, etc.
- Sécurité : générer un secret pour garantir la confidentialité
Dans les deux domaines, la qualité du générateur est importante. Si un générateur est biaisé, c'est-à -dire que la distribution n'est pas équitable entre les différentes valeurs possibles, le résultat de la simulation sera invalide (ou bien simplement imprécis) et la confidentialité peut être comprise. Par contre, la simulation privilégie la vitesse du générateur. Alors que pour la sécurité on se donne les moyens pour qu'il soit difficile de deviner les nombres précédemment générés et les prochains nombres générés (quitte à ce que le générateur soit plus lent), ce qui revient à deviner quel est l'état interne du générateur étant donné qu'un algorithme est déterministe.
Générateur biaisé
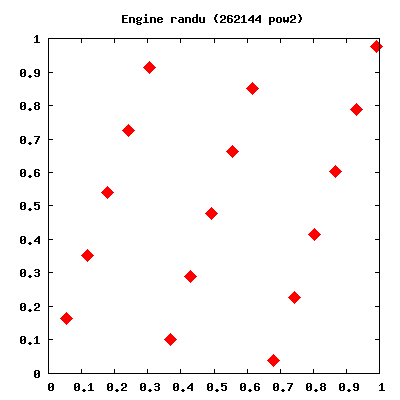
Reprenons l'exemple de RANDU, un générateur biaisé (les bits de poids faible sont peu aléatoires). Si on utilise 1 + rand() % 6 pour simuler un lancé de dé, on va obtenir une suite du genre :
1, 3, 1, 5, 3, 3, 1, 5, ...
Les faces 2, 4 et 6 ne sont jamais tirées !
Inverser un générateur congruentiel linéraire
Il est possible de deviner l'état interne d'un générateur congruentiel linéraire (LCG) en ne connaissant qu'un seul nombre généré. L'algorithme RANDU est :
x(n+1) = (x(n) * 65539) % 2147483648
Avec x(0) : graine du générateur. On peut exécuter le générateur à l'envers en calculant :
y(n+1) = (y(n) / 65539) % 2147483648
Sachant que diviser revient à multiplier par l'inverse, x / 65539 <=> x * (1 / 65539), on va calculer l'inverse 65539 modulo 2147483648 avec le théorème des restes chinois. En pratique, on utilise l'identité de Bezout. Fonction Python qui calcule les coefficients u et v tels quel a · u + b · v = 1 :
def bezout(a, b):
u0 = 1; u1 = 0
v0 = 0; v1 = 1
while 1:
q = a // b
r = a % b
u0, u1 = u1, u0 - q*u1
v0, v1 = v1, v0 - q*v1
if r != 0:
a = b
b = r
else:
break
return (u0, v0)
On calcule alors bezout(65539, 2147483648) = (477211307, -14564), ce qui donne :
65539 · 477211307 - 2147483648 · 14564 = 1
et
(477211307 * 65539) % 2147483648 = 1
Finalement, y(n+1) = (y(n) * 477211307) % 2147483648.
Exemple :
x(0) = 42 x(1) = 2752638 x(2) = 16515450 x(3) = 74318958
On utilisant x(3), on va pouvoir générer les nombres précédents :
y(0) = 74318958 y(1) = 16515450 y(2) = 2752638 y(3) = 42
On a donc réussi à retrouver les nombres précédents jusqu'à la graine (42). Même si le générateur ne délivre que quelques bits de son état interne (ex: rand() = x(n) & 0xffff), on peut retrouver l'état interne en utilisant une recherche exhaustive (si on dispose de quelques nombres successifs).
Solutions
Pour rééquilibrer la distribution d'un générateur, on peut l'améliorer en utilisant différrentes techniques :
- Utiliser la parité du flux
- Utiliser le mapping de transition (technique de Von Neumann)
- Utiliser la transformée de Fourier discrète (ou une transformation de Fourrier rapide, FFT)
- Utiliser la compression (en zappant les entêtes et autres parties « fixes »)
Lire la RFC 1750 pour les sources et les détails sur ces techniques.
Pour empêcher qu'un pirate arrive à deviner l'état interne du générateur, on peut rajouter une fonction de hachage sur la sortie du générateur (ex: MD5, SHA-1, ...). Il est toujours possible d'inverser la fonction de hachage, mais c'est beaucoup plus difficile !